1. 백트래킹(Backtracking)
가장 대표적으로 알고 있는 완전 탐색 알고리즘으로는 DFS를 꼽을 수 있습니다. 하지만 DFS는 정말 완전히 모든 경로를 탐색하므로, 때때로 비효율적일 수 있습니다. 여기서 백트래킹이라는 개념이 등장합니다. 바로 가능성이 있는 부분만 탐색한다는 것입니다. 즉, 어떤 노드를 탐색할 때, 목표로 가는 가능성이 없는 노드라면, 과감하게 배제하고 되돌아갑니다. 이를 가지치기(Pruning)이라고 합니다.
이해를 돕기 위해 예시를 이용해 설명을 더 해보도록 하겠습니다. 백트래킹을 설명할 때 가장 많이 사용하는 예시는 바로 N-Queen입니다.
2. N-Queen
N-Queen 문제는 다음과 같이 설명할 수 있습니다.
"크기가 N*N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제"
체스에서 퀸은 자신이 존재하는 위치를 기준으로 상하좌우 그리고 대각선까지 칸의 개수에 상관없이 이동할 수 있는 공격력 최강의 말입니다. 아래는 나무 위키에서 가져온 퀸의 이동 가능 위치입니다.
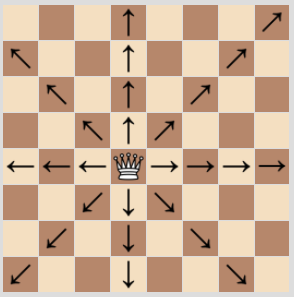
이제 N개의 퀸을 서로 공격할 수 없는 문제를 해결해보도록 하겠습니다.

위의 그림처럼 (1,1)에 퀸을 놓으면 빨간색 줄이 그려진 칸으로는 모두 빨간 퀸이 이동할 수 있기 때문에 나머지 자리들에만 퀸을 놓을 수 있습니다. 즉 (1,1)에 퀸을 놓으면 검은색 퀸이 그려진 자리에만 퀸을 놓을 수 있다는 뜻입니다. 이런 식으로 퀸들을 계속해서 서로를 공격할 수 없는 위치에 놓아줍니다.

위 그림처럼 퀸 끼리 서로를 공격할 수 없는 위치에 N개의 퀸을 놓을 수 있습니다. 이는 N개의 퀸을 서로를 공격할 수 없도록 놓는 여러 경우의 수 중 하나일 뿐입니다. 이 N개의 퀸을 놓는 경우의 수를 구하는 것이 바로 N-Queen 문제입니다.
3. N-Queen의 구현

(1,1)에 퀸을 하나 놓는다고 가정해 보겠습니다. 그렇다면 위의 트리 구조와 같이 (2,1) ~ (2,5)까지 2행에 놓을 수 있는 경우의 수가 생깁니다. 여기서 저희는 아예 불가능 한 곳인 (2,1)과 (2,2)를 배제할 수 있습니다. 만일 DFS로 수행한다면, 불가능한 곳들도 모두 탐색을 할 것이고 이는 메모리나 시간적으로 많은 비효율을 야기하게 됩니다.
바로 위에서 언급한 아예 불가능 한 곳인 (2,1)과 (2,2)를 배제하는 과정을 바로 가지치기라고 부릅니다. 이 가지치기를 얼마나 잘하느냐가 구현한 백트래킹 알고리즘의 성능을 결정하게 됩니다.
N-Queen은 다음과 같은 절차를 따릅니다.
1. DFS처럼 탐색을 시작
2. 방문한 노드가 가능성이 있는 노드인지를 검사.
3. 가능성이 있는 노드이면 재귀를 통해 다음 노드로 넘어가고, 그렇지 않으면 백트래킹을 수행.
이 절차를 수행하면 가능성이 없는 칸들을 모두 배제하고 퀸이 놓아질 수 있는 총 경우의 수를 얻을 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
import java.io.*;
class Main {
static int N;
static int[] col;
static int cnt = 0; // 몇 개의 경로가 만들어지는지 저장
public static void backtracking(int row) {
if (row == N) { // 체스판의 끝에 도달했다면
cnt++; // 해당 경로가 존재하는 것이므로 cnt + 1
} else {
for (int i = 0; i < N; i++) { // 해당 행의 모든 노드를 검사
col[row] = i;
if (is_possible(row)) { // 가능성이 있는 노드라면
backtracking(row + 1); // 한 단계 더 내려가서 재귀 실행
}
}
}
}
public static boolean is_possible(int row) {
for (int i = 0; i < row; i++) { // 자신보다 위에 이미 결정된 퀸의 위치들을 모두 확인하며
if (col[row] == col[i] || col[row] == col[i] + row - i || col[row] == col[i] - row + i) {
return false; // 같은 열에 있거나 대각선 상에 존재하는 경우에는 false를 리턴
}
}
return true;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
N = Integer.parseInt(br.readLine());
for (int i = 0; i < N; i++) { // 첫 번째 줄
col = new int[N]; // col 배열에는 각 행 별로 선택된 노드를 저장
col[0] = i; // 첫 칸에는 i
backtracking(1); // 다음 행 부터 탐색 시작
}
bw.write(String.valueOf(cnt)); // 최종 카운트 갯수 출력
bw.flush();
bw.close();
br.close();
}
}
|
cs |
'전공공부 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [알고리즘] 완전탐색 (0) | 2022.02.08 |
|---|---|
| [알고리즘] 코사라주 알고리즘 (0) | 2021.12.29 |
| [알고리즘] 다익스트라 알고리즘 (0) | 2021.03.03 |
| [알고리즘] KMP 알고리즘 (0) | 2021.02.25 |
| [알고리즘] 다이나믹 프로그래밍 (0) | 2021.02.04 |