반응형
개인적인 풀이일 뿐, 최적의 정답이 아님을 알려드립니다.
문제
1806번: 부분합
첫째 줄에 N (10 ≤ N < 100,000)과 S (0 < S ≤ 100,000,000)가 주어진다. 둘째 줄에는 수열이 주어진다. 수열의 각 원소는 공백으로 구분되어져 있으며, 10,000이하의 자연수이다.
www.acmicpc.net
난이도: 골드 4
사용언어: JAVA
풀이
이 문제는 두 개의 포인터를 이용하여 해결할 수 있습니다. 수열에서 연속된 수들의 부분합 중에 그 합이 S를 넘는 것 중, 가장 짧은 것을 찾는 것이 문제이기 때문에, 연속된 수들의 첫 부분과 마지막 부분을 포인터로 가리키고, 이 두 포인터를 적절히 증가시키며 최소 길이를 구할 수 있습니다.
주어진 예제를 이용해 설명을 진행하겠습니다.

위의 값들을 배열에 담고, 두 개의 포인터를 준비해줍니다. 그 뒤에 아래와 같은 순서를 따릅니다.
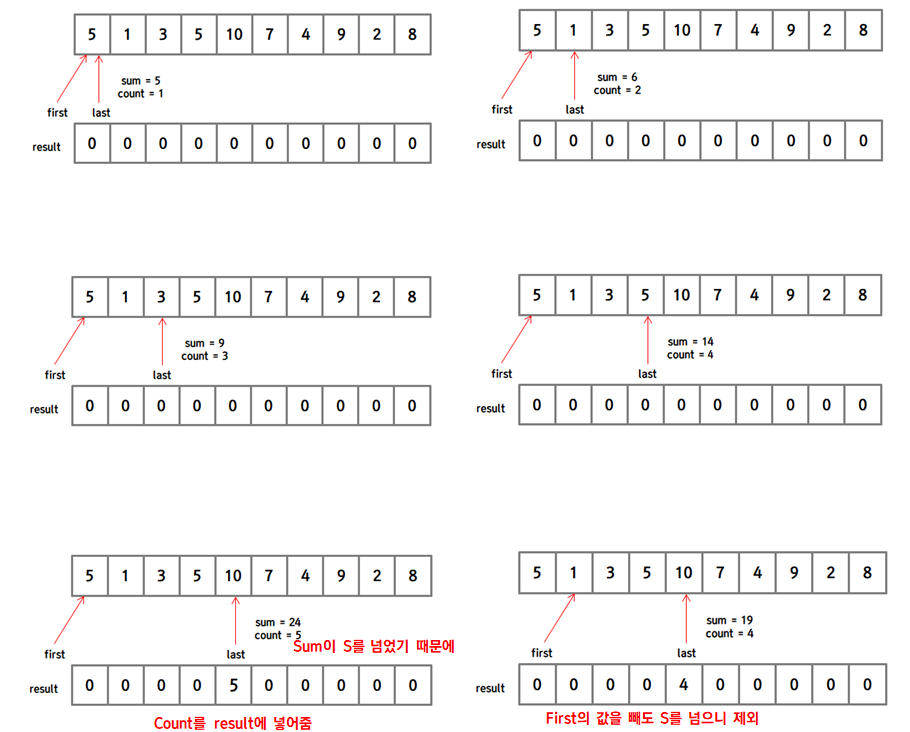

위의 그림과 같이 두 개의 포인터를 이용해 결과를 result라는 배열에 담을 수 있고, 최종적으로 result에서 0을 제외한 가장 작은 값을 정답으로 출력시켜주면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String s = br.readLine();
StringTokenizer st = new StringTokenizer(s);
int N = Integer.parseInt(st.nextToken());
int S = Integer.parseInt(st.nextToken());
int i;
int first = 0;
s = br.readLine();
st = new StringTokenizer(s);
int[] arr = new int[N]; // 입력을 받는 배열
int[] result = new int[N]; // 결괏값을 저장하는 배열
int sum = 0, cnt = 0;
for (i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
sum += arr[i];
if (arr[i] > S) { // 만일 한 숫자가 S보다 크다면 뒤는 더 볼 필요도 없이 정답은 1
bw.write(String.valueOf('1'));
bw.flush();
System.exit(0);
}
cnt++;
if (sum >= S) { // sum이 S보다 크다면,
while (sum >= S) { //first를 한 칸씩 전진시키면서 S보다 큰지를 확인
sum -= arr[first++];
cnt--;
}
sum += arr[--first];
cnt++;
result[i] = cnt; // result 배열에 cnt 저장
} else { // sum이 S보다 작다면,
result[i] = 0; // 0 저장
}
}
Arrays.sort(result); // 소팅을 수행해서,
for (i = 0; i < N; i++) {
if (result[i] != 0) { // result에서 0이 아닌 가장 작은 값 출력
bw.write(String.valueOf(result[i]));
bw.flush();
System.exit(0);
}
}
bw.write('0'); // S를 넘길 수 있는 조합이 없다면 0을 출력
bw.flush();
}
}
|
cs |
반응형
'백준 온라인 저지 > Gold' 카테고리의 다른 글
| [BOJ] 2352 - 반도체 설계 (0) | 2021.02.22 |
|---|---|
| [BOJ] 5427 - 불 (0) | 2021.02.21 |
| [BOJ] 2056 - 작업 (0) | 2021.02.21 |
| [BOJ] 1915 - 가장 큰 정사각형 (0) | 2021.02.20 |
| [BOJ] 17298 - 오큰수 (0) | 2021.02.20 |